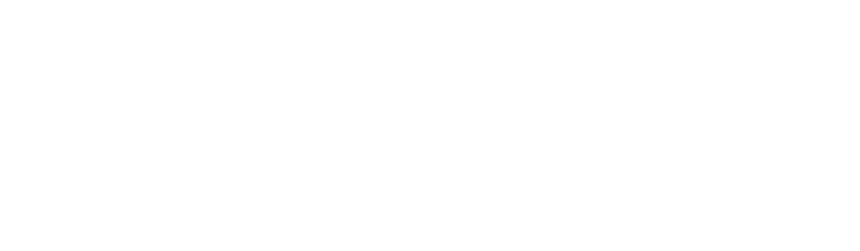Synonyme d’harmonie, le nombre d’or (phi) se retrouve dans l’architecture, la musique, la peinture, l’informatique, le vivant…

Il est utilisé pour définir des formes ou des proportions “élégantes”.

Côté maths

• C’est un nombre réel noté ϕ (phi) et sa valeur vaut : ϕ = (1 + √5) / 2 ≈ 1,618…
• C’est l’unique racine positive de l’équation polynomiale : X^2 = X + 1. On dit que c’est un nombre irrationnel algébrique.
• C’est aussi la limite du rapport F(n+1) / F(n), où F(n) est le n-ième terme de la suite de Fibonacci définie par :
  
  • Deux premiers termes : 0, 1
  • Termes de rang n > 1 : F(n) = F(n-1) + F(n-2)
    
    • Voici le début de la suite : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.

Objets dérivés

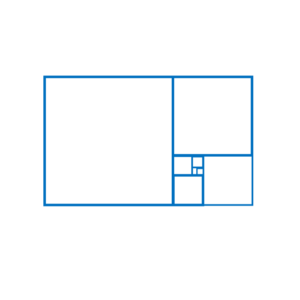
Rectangle d’or

Rectangle vérifiant la proportion :

• (longueur / largeur) = (longueur + largeur) / longueur = ϕ

Construction :

• Faire un carré
• Tirer un segment entre le milieu d’un côté et l’un des sommets opposés. Ce segment est le rayon d’un cercle.
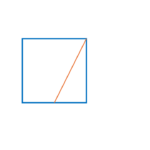
• Prolonger le cercle (qui passe forcément par deux sommets du carré) jusqu’à trouver l’intersection avec l’horizontale
• Le rectangle est ainsi déterminé : sa largeur est le côté du carré, et sa longueur est la distance séparant la base du carré jusqu’à l’intersection faite précédemment
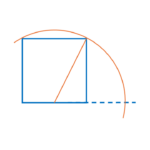
• On remarque que si vous placez un carré dans un rectangle d’or, le reste du rectangle est un autre rectangle d’or.
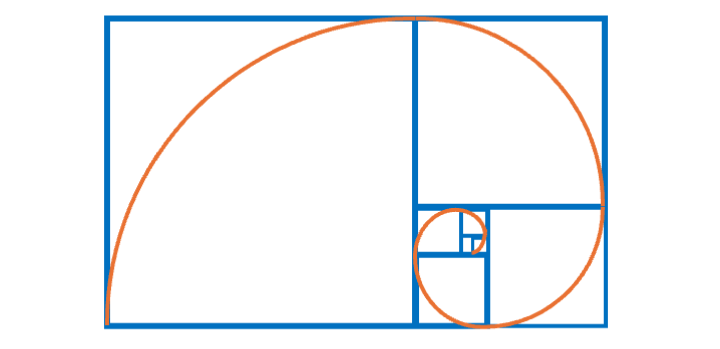
• Si on fait passer un quart de cercle par chacun de ces carrés (inscrits dans les rectangles d’or successifs), on obtient une spirale dorée (cf. ci-dessous)

Triangle d’or

Triangle isocèle vérifiant la proportion : côté / base = ϕ

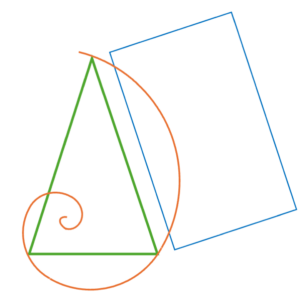
Spirale d’or

Une spirale d’or est construite par des quarts de cercle inscrits dans les carrés constitutifs de rectangles d’or

• Son équation polaire est : r(θ) = r.ϕ^(2θ/𝛑)
• Son amplitude s’accroît d’un facteur ϕ à chaque fois qu’elle décrit 90°
• La forme de l’oreille humaine serait une bonne représentation de spirale dorée

Usage “pratique“ en photo

La règle des tiers est dérivée (en première approximation) de la proportion d’or. En première approximation seulement, car le rapport 3/2 sur lequel se fonde la règle des tiers n’est pas tout à fait égal à φ = 1,618…ce qui n’est pas étonnant car cela revient à ne considérer que les premiers termes de la suite de Fibonacci alors que φ est évalué à l’infini de celle-ci.

C’est finalement une sorte de principe naturel selon lequel un cadre apparaît comme plus vivant, plus harmonieux, plus rythmé lorsqu’il existe une dissymétrie tendant à regrouper les lignes et éléments forts d’un plan suivant des lignes particulières dites “lignes de force” et de leurs intersections dites “points forts”.

Pour tout cadre (peinture, photographie, plan cinématographique fixe ou panoramique…), il existe donc 4 lignes de force et 4 points forts sur lesquels l’œil humain se tourne spontanément. Ces lignes de force correspondent à un découpage en 3 tiers suivant l’horizontale et suivant la verticale. Les points forts sont tout simplement l’intersection d’une ligne de force horizontale et d’une ligne de force verticale. Voici la position de ces lignes et points :

Maintenant, il convient de se rappeler que pour mettre en valeur un élément d’une scène, il sera très souvent plus judicieux de cadrer de telle sorte que l’élément en question se retrouve sur une ligne de force voire sur un point fort.

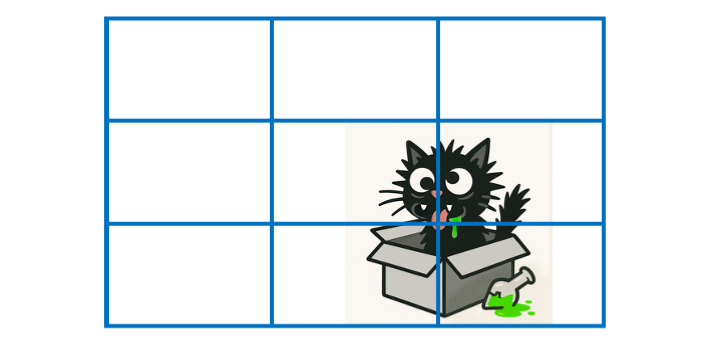
Exemples : une ligne d’horizon d’un paysage devra (dans 90% des cas) coïncider avec une ligne de force horizontale ; celle du bas si on veut mettre le ciel en valeur, celle du haut si on veut mettre la terre en valeur. De même, un arbre, un poteau, une pancarte, les bords d’un bâtiment devront la plupart du temps coïncider avec une ligne de force verticale.

Un objet qui se déplace vers la droite (respectivement gauche) a tout intérêt à se trouver sur la ligne de force de gauche (respectivement droite) pour laisser de l’espace “utile”. Même chose pour une personne regardant vers la droite (respectivement gauche).

Pour interviewer une personne, on prendra soin de positionner le visage (les yeux surtout) de celle-ci au niveau d’un point fort.

À vous d’adapter cette règle ou de la contourner volontairement suivant la situation. En effet, on pourra parfois centrer volontairement le sujet de l’image pour jouer sur des symétries ou évoquer une impression de solennité.

Comme mentionné plus haut, il convient toutefois de distinguer la règle des tiers et la règle dite des “proportions d’or”. Concrètement, les divisions du cadre en proportions d’or s’obtiennent en resserrant les lignes vers le centre. Au doigt mouillé, sur des écrans au format approximativement 16:9, vous pouvez deviner les verticales d’or en imaginant un carré sur le bord droit (cf. carré vert) ou gauche (cf. carré orange). L’autre côté du carré vous donnera une verticale située à peu près sur la proportion dorée.

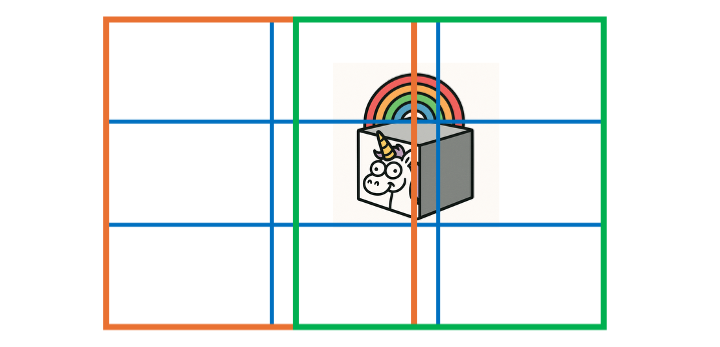
La différence est subtile, mais a le mérite d’exister. Un cadre pris suivant les proportions d’or plutôt que la règle des tiers rapproche un peu plus les éléments vers le centre, leur donnant ainsi plus de stabilité et d’équilibre, sans pour autant centrer l’image.

La règle d’or sera plus adaptée à des paysages avec des lignes d’horizon (la règle des tiers peut avoir tendance à créer un trop fort déséquilibre). Encore une fois, c’est du feeling…

Et le nombre d’or dans Malgovert ?

Même si j’utilise régulièrement les règles des tiers ou les proportions dorées pour mes illustrations, le nombre d’or n’apparaît pas en tant que tel dans la trilogie Malgovert. Du moins, pas directement. Néanmoins, j’utilise à plusieurs reprises les termes de la suites de Fibonacci, en particulier : 5, 8 et 13.

Ces termes ont pour moi une très forte symbolique que j’exploite à fond durant toute la trilogie.

• 5 : les éléments, les fleuves infernaux, les pièces fortes d’un d’échec
• 8 : la lemniscate de Bernoulli (symbole de l’infini) et le chiffre de la boule de billard noire.
• 13 : les constellation du Zodiaque